Krek se je skliceval na profesorja Milana Batisto, ki je skupaj s kolegi na Inštitutu za promet in pomorstvo Univerze v Ljubljani uporabil dva modela. Obrnili smo se na profesorja, ki nam je pojasnil nekaj podrobnosti.

Po izobrazbi ste strojnik, in ne zdravnik ali epidemiolog.
Res je, ampak tisto, kar znam, je uporabna matematika in epidemiološki modeli so matematični modeli in ne klinična epidemiologija. Ne nazadnje se ne spuščam v zdravljenje in ukrepe itd., ampak gledam model in podatke. In za zdaj model dobro kaže ukrepe in to je največ, kar lahko od dobrih modelov pričakujemo.
Za ljubitelje teorije
Zakaj in kako ste se sploh lotili tega modela?
Mene in kolege na Inštitutu za promet in pomorstvo je zanimal vpliv izbruha epidemije na Kitajskem na promet z EU-jem in predvsem Luko Koper. Za oceno gibanja števila okuženih smo uporabili dva znana epidemiološka modela. Logistični model (star 200 let) v nasprotju z eksponentno rastjo upošteva tudi drugo stran krivulje – eksponentno umirjanje (okuženi namreč ne more več okužiti okuženega) in klasični model SIR (star 100 let), ki populacijo razdeli na prenašalce, okužene in ozdravljene. Opazili smo, ko je epidemija pod kontrolo, oba modela težita k isti vrednosti končnega števila okuženih. V primeru Kitajske smo konec februarja naredili oceno 83.000, zdaj je to število malo pod 82.000. Opazili pa smo, da se podatki počasi odlepljajo od krivulje – posledica je bil izbruh pandemije. To nam je dalo idejo, da v bistvu lahko s sprotnim spremljanjem podatkov in modela vidimo učinek ukrepov.
Model oziroma metodo smo konec februarja objavili v kratkem članku na medicinskem portalu medRxiv. Članek ima do zdaj okoli 5000 ogledov. Nekatere njegove dopolnitve pa so imele nenavadno visok odziv na portalu ResearchGate. Programska orodja za spremljanje pa na Matlabovem portalu za izmenjavo programov (trenutno zasedamo osmo mesto med 15.000 programerji). Eden izmed njih je bil pred kakšnimi 14 dnevi celo izbran za program tedna.

Zakaj ste izbrali prav ta modela? Ste se s kom posvetovali?
Izbrali smo ju zaradi primerjave rezultatov. Obstaja kopica modelov, izbrana pa sta najpreprostejša in najstarejša in nekako dobro odslikujeta potek epidemije: eksponentna rast, pospešena rast, eksponentno umirjanje in konec. Ker je osnovna ideja v dnevnih napovedih, nima smisla uporabljati bolj zapletenih modelov, oba modela pa tudi ne zahtevata vrste različnih podatkov ‒ potrebujeta le skupno število okuženih.
Krivulja je v precej državah zelo podobna, čeprav ukrepi povsod niso bili enaki oziroma v istem časovnem intervalu?
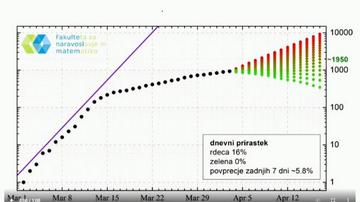
Krivulje si seveda niso podobne za vse države. Iz krivulj se natančno vidi, kje so pravočasno uvedli karanteno in kje ne (oziroma ali je model primeren ali ne). S karanteno se približamo pogojem modela (zaprta populacija in enakomerno mešanje); v odprtih populacijah model SIR ne deluje in ni primeren za kontrolo in napovedovanje. Tole je primer Kitajske, ki je uvedla strogo karanteno.
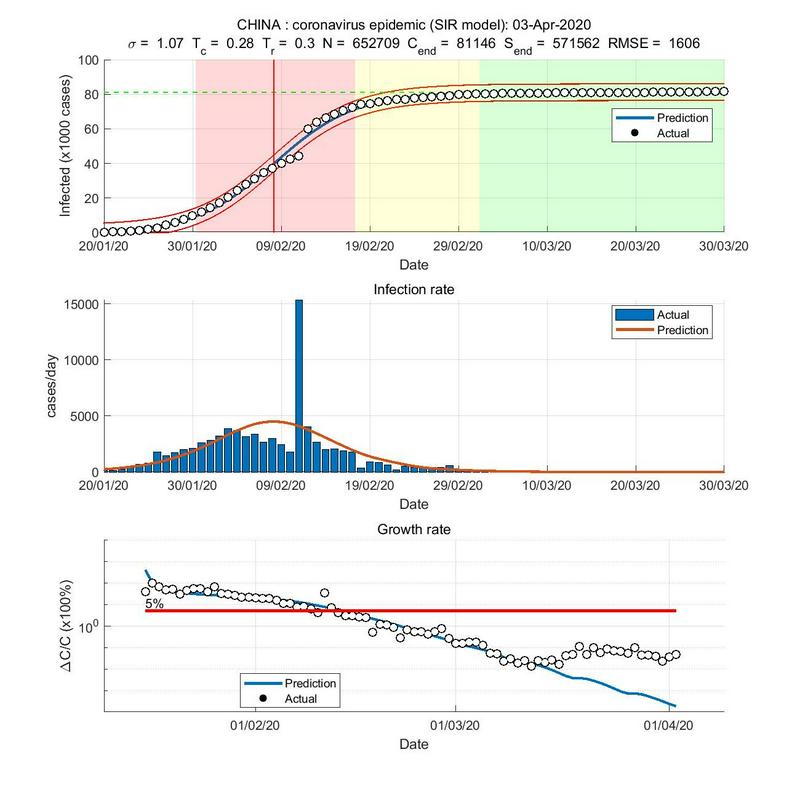
Tole je primer Južne Koreje, kjer jim zadeva uhaja izpod nadzora (vsak dan imajo namreč približno konstantno število okuženih med 50 do 100), krivulja se dviga, vendar (še) ne prihaja do izbruha.
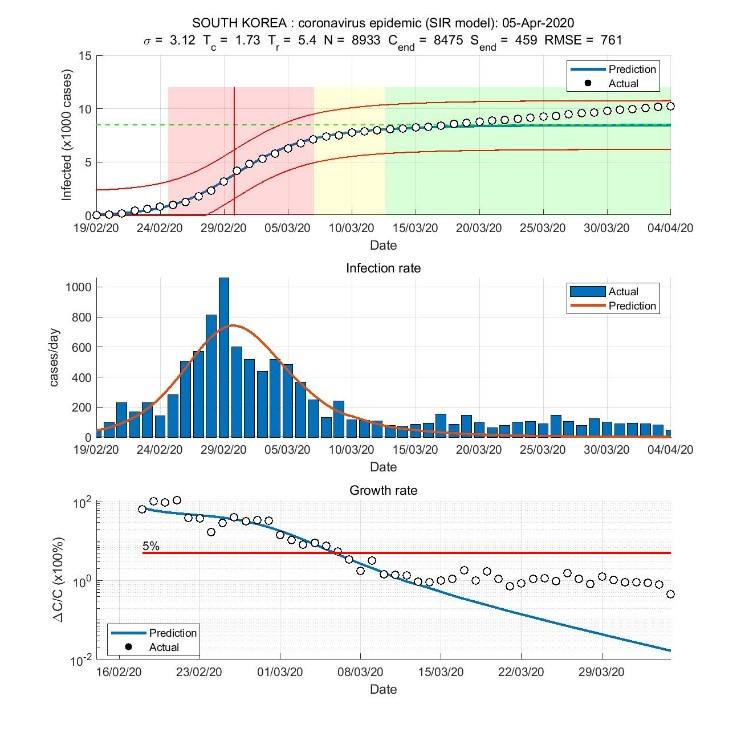
Tole je Avstrija, kjer karantena deluje, krivulja napovedi je skoraj idealna.
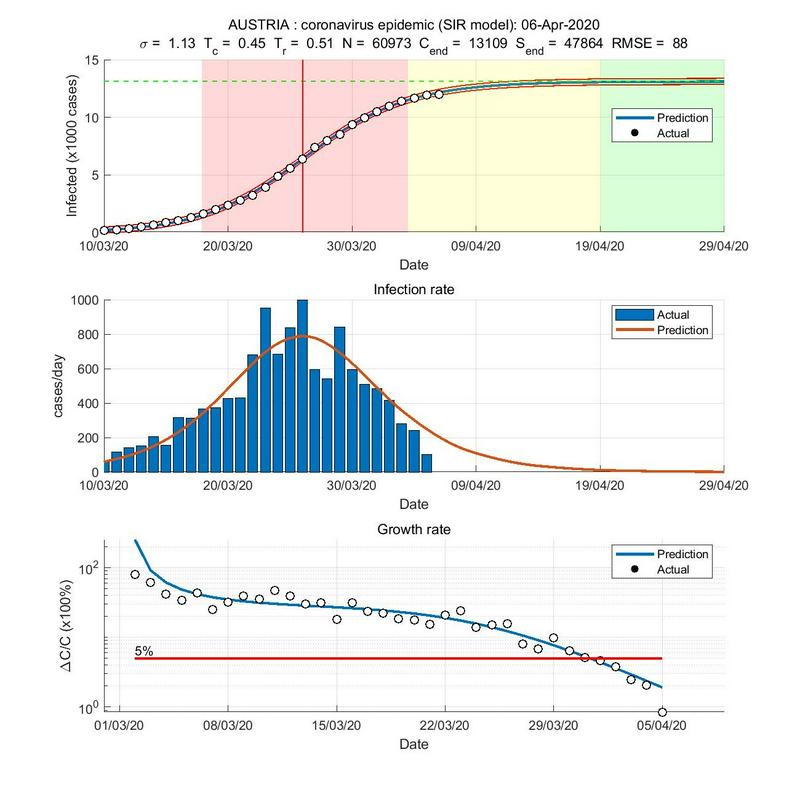
Tole pa je Danska, kjer so očitno ignorirali prvi izbruh in se jim bo na podlagi te napovedi zadeva še kar vlekla.
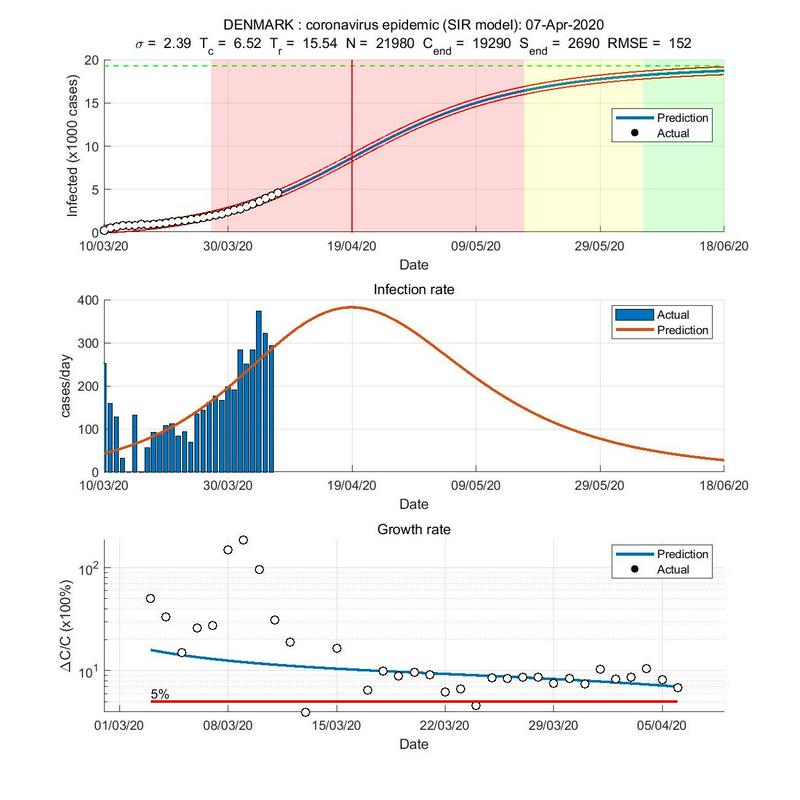
Ali model, ki ste ga uporabili, kar koli pove o dejanskem številu okuženih (to število je precej višje)?
Ne. Model pa pove, koliko je kontaktno število, kolikšna je množica latentno kužnih, koliko bo mogoče končno število kužnih in koliko bo ostalo latentno kužnih. Seveda se te napovedi dnevno spreminjajo. Iz njih pa vidimo trend. Za Slovenijo so trendi naslednji.
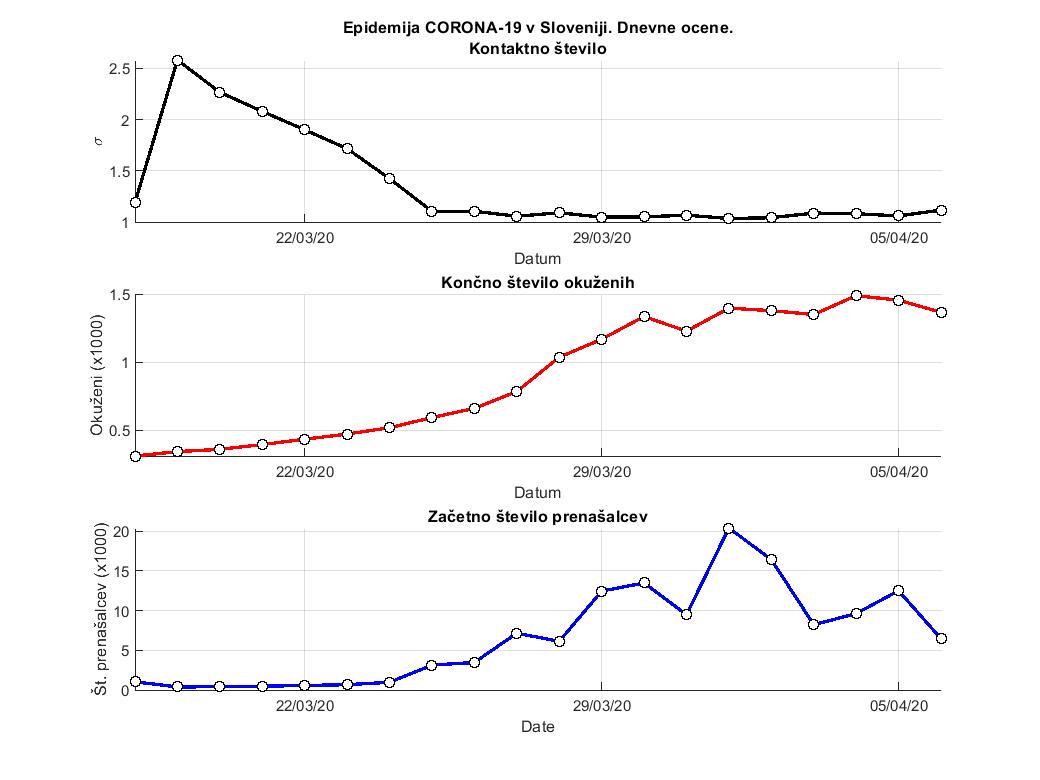
Ali bi v ta model lahko vnesli hipotetičen primer, da bi se vsi prebivalci ta hip nehali držati ukrepov, do kakšne številke okužb bi prišli?
Ne, model je izdelan za sprotno spremljanje. Tehnično to pomeni, da vsak dan z novimi podatki računamo parametre modela in naredimo napovedi. Simulacijski modeli so drugačni. Tam se vrednosti parametrov predpostavijo in se pogleda, kakšne so posledice. Teh modelov je trenutno polno po vsem spletu.
Model je dal napoved za Slovenijo o približno 1.600 uradno okuženih osebah ob koncu pandemije. Kdaj ste ga prvič zagnali in za koliko odstotkov se ločijo dnevne napovedi od dejanskih okužb?
Gre za dnevno spremljanje števila okuženih, kot vreme, in dnevne napovedi. Bliže smo cilju, boljše so napovedi. Vendar pa glavni namen modela niso dnevne napovedi skupnega števila okuženih, čeprav so zdaj znotraj treh odstotkov, ampak dolgoročna dnevna napoved (napoved dnevnega števila okuženih je seveda bistveno slabša). Ko bo ta konstantna, bo epidemija pod kontrolo (kot kaže zgornja slika za Kitajsko).
Takole so videti dnevne napovedi za Slovenijo (ocenjena napaka je +/- 8 okuženih za 1 sigma) narejene z 2-valnim logističnim modelom.
| Datum | Napoved | Prava številka | Napaka (%) |
| 28. marec | 676 | 684 | 1,2 |
| 29. marec | 735 | 730 | 0,7 |
| 30. marec | 784 | 756 | 3,7 |
| 31. marec | 807 | 802 | 0,6 |
| 1. april | 840 | 841 | 0,1 |
| 2. april | 871 | 897 | 2,9 |
| 3. april | 913 | 934 | 2,2 |
| 4. april | 957 | 977 | 2,0 |
| 5. april | 994 | 997 | 0,3 |
| 6. april | 1021 | 1021 | 0,0 |
| 7. april | 1043 | ? | ? |
Ali ste delali tudi na projekciji števila umrlih?
Ne. Namen programa je bil, da ljudem pokažemo luč na koncu predora, zato smo namenoma izpustili oceno umrlih. Je pa to oceno vključil kolega iz ZDA, ki je priredil naš program za njihove potrebe.

Milan Krek je ocenil, da bi brez ukrepov umrlo 90.000 ljudi. Je to njegova ali vaša ocena?
Mislim, da gre za zelo preprosto oceno. Če bi se namreč naključno mešalo vseh 2 milijona prebivalcev Slovenije in bi vsi zboleli, smrtnost pa je 5 odstotkov, potem bi nas umrlo 100 tisoč.
Kako ste prišli v stik s Krekom?
Pred kakimi 14 dnevi smo v Primorskih novicah objavili kratek prispevek o poteku epidemije in napovedih. Po tistem me je gospod Krek poklical.
Če prav razumem, glavna ideja uporabe te metode ni določiti popolnoma natančno končno številko okuženih, ampak opozoriti na pozitivne učinke spoštovanja karantene? Je to uporabna vrednost?
Ideja je nekako taka, kot ste povedali. Gre za to, da primerjamo stanje z napovedjo modela in če se razhajata, je nekaj narobe (krivulja se spreminja) oziroma se epidemija še razvija, če pa se napoved in model ujemata, potem vemo, kako bo epidemija potekala oziroma jo imamo pod nadzorom (krivulja je vedno ista). Kakšni ukrepi so potrebni, je druga stvar oziroma to ni stvar modela. Očitno pa je na Kitajskem in tudi drugje, vsaj dokler ni cepiva ali zdravila, karantena najučinkovitejši ukrep, to so vedeli že v srednjem veku, če ne že prej.
Obvestilo uredništva:
Zaradi številnih komentarjev in zagotavljanja čim višjih standardov razprave pod članki o novem koronavirusu smo se odločili, da komentiranje na portalu rtvslo.si omogočimo pod omejenim številom novic. Svoje mnenje o dogajanju v povezavi z novim koronavirusom lahko ob spoštovanju forumskih pravil MMC RTV SLO izrazite v komentarjih tukaj.




















































 2. sv
2. sv